Siguiendo con el dibujo anterior, en la tercera figura, la inferior, aún tenemos que eliminar tanto el volumen marcado en rojo, como el amarillo (aunque no se aprecia volumen, pues es una captura de la planta ancha)
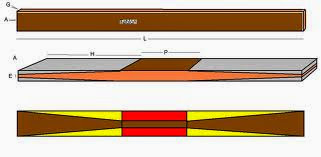
Para el Rojo es fácil, pues serían dos piezas de (P x G x Eje menor de la pértiga)
Calculo para Em (Eje menor) = 3 cm.
así quedaría
50 x 3,8 x 3 = 570 ml. como dos eliminaríamos 1.140 ml. aplicando la densidad quedan 456 g. que debemos descontar al tablón tal y como está en este momento:
2.245 - 456 = 1.789 g.
Seguimos con más de kilo y medio, algo pesado para este tipo de palas ¿no?
Veamos la evolución en el peso de las piezas eliminadas:
Cuñas grises = -765 g. lo que es un 25,4% del peso total del tablón inicial.
Volumen rojo = -456 g. sería un 15,1 % del tablón
Me da a mí que supongo bien al pensar que todo lo demás que vayamos a eliminar irá descendiendo su peso, es decir, lo más grodo lo sacamos al diseñar las cuñas grises iniciales. Y nunca más en el proceso deberíamos poder quitar tanta madera.
¿Iré bien orientado con esa suposición?
Ahora viene donde no doy continuado, y creo que sería el punto donde a partir de ahí ya poca madera le vamos a quitar, por mucho que afilemos aristas, redondeemos cantos, lijemos, etc...
Hombre, gramito por aquí gramito por allá, pues claro que reduciremos, pero no podemos esperar eliminar un peso considerable. Por lo tanto a título orientativo creo que podría tomarse como el fin de tal cálculo orientativo.
Vamos pues a donde las formas del volumen a eliminar me hacen chocar contra un muro.
Veamos un dibujo que quizá nos dé una mejor visión del problema.

Esas nuevas cuñas verdosas no consigo encajarlas mentalmente para ver si logro una forma cúbica más o menos sencilla que me permita aplicar una fórmula simple para calcular su volumen.
En mi planteamiento quedaría que:
G = 3,8 = Eje mayor de la pértiga (EM)
Y el eje menor (Em) lo he fijado en 3 cm.
Luego, esas cuñas verdes, una vez cortadas, si una la colocamos con la parte rayada a modo de base (como se observa o intenté hacer ver en la figura inferior de este segundo dibujo) veremos que su altura sería de 3 cm. pues aplicando la fórmula (A - Em)/2 así resulta --> 9-3= 6 entre 2 pues 3

Y el ángulo formado entre esa base (verde rayada) con la cara gris es, lógicamente, un ángulo recto.
¿Alguien daría calculado ese volumen generado por las cuñas verdes?
¿Podríamos eliminar otro 15% del peso al cortar esas cuñas verdes? ¿Más incluso, o menos quizás?
Finalmente, y tras analizarlo, tampoco tenemos que comernos tanto el coco

pues podríamos llevar como regla la idea que ha comentado Koe, es decir, partir de que con un tablón de esas medidas (220x9x3,8) debería rondar los 2 kilos 600 g.
Si pesa 3 Kg. ya sabemos que nos saldrá una pala más bien pesada.
Ahora esa regla habría que analizarla y sacar alguna fórmula para dependiendo del tablón que nos cedan en la carpintería, según su tamaño y pesándolo, quizá con una sencilla regla de tres ver cuánto pesaría el tablón base de 220x 9 x 3,8
Imaginemos que llegas al carpintero y tiene tablones de 600 x 20 x 10 ¿cuánto debería pesar (cosa que podemos comprobar allí sin ningún compromiso), antes de decidir comprarlo y que te lo corten a las medidas requeridas para que el tablón base del cual saldrá una pala pese en torno a 2,6 Kg?
Bueno, siempre puedes calcular su densidad, es una solución, multiplicas sus tres medidas, lo pesas y te da fácilmente su densidad. Si ves que anda en torno a 0,35 g/ml sabrás que te saldrá una pala ligera.
A lo mejor me estoy complicando para nada ¿cómo lo veis?

PD: Si alguien sabe cómo calcular el volumen de las cuñas verdosas que me lo diga, explique, porque sea como sea me interesa, cuestión de amor propio quizá
